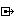More ...
編集履歴:過去のバージョン
2015/09/08 23:00:54 JST時点での数式の文字列を計算するモジュール(一度逆ポーランド記法に変換)の内容
* スクリーンショット [[$$img https://cloud.githubusercontent.com/assets/6854255/9295522/9c3ee9fa-44ab-11e5-9b58-5edc82371162.png]] [https://cloud.githubusercontent.com/assets/6854255/9295522/9c3ee9fa-44ab-11e5-9b58-5edc82371162.png 拡大] * calc.hsp {{{ #module c // 演算子の優先順序 // 低い #enum UNKNOWN = -1 #enum PAREN // 括弧は例外 #enum XOR_ #enum OR_ #enum AND_ #enum LESS #enum GRTER #enum EQUAL #enum ADD #enum SUB #enum MULT #enum DIV #enum POW // 高い #define stack(%1,%2) sdim %1,20,%2:%1_i=0 #define push(%1,%2) %1(%1_i)=%2:%1_i++ #define ctype pop(%1) _pop@c(%1(%1_i-1),%1_i) #defcfunc local _pop var val, var index index-- return val #define logstack(%1) _tmp="%1:":repeat %1_i:_tmp+=%1(cnt)+",":loop:logmes _tmp // 計算を行う #defcfunc calc str f // 逆ポーランド記法でスタックpriに計算式を積む import f // 浮動小数点数で計算するかどうか is_double = 0 repeat pri_i token = pri(cnt) // 小数点が含まれていればそれ以降浮動小数点として扱う is_double |= (instr(token, 1, ".") != -1) if ( to_ope(token) == UNKNOWN ) { // 数値なら push sec, token } else { // 演算子なら // 左辺、右辺を取得 right = pop(sec) left = pop(sec) // 文字列から変換 if (is_double) { right = double(right) left = double(left) } else { right = int(right) left = int(left) } // 計算処理 switch(to_ope(token)) case XOR_ push sec, str(int(left) ^ int(right)) swbreak case OR_ push sec, str(int(left) | int(right)) swbreak case AND_ push sec, str(int(left) & int(right)) swbreak case LESS push sec, str(left < right) swbreak case GRTER push sec, str(left > right) swbreak case EQUAL push sec, str(left == right) swbreak case ADD push sec, str(left + right) swbreak case SUB push sec, str(left - right) swbreak case MULT push sec, str(left * right) swbreak case DIV is_double = 1 push sec, str(double(left) / double(right)) swbreak case POW push sec, str(powf(left, right)) swbreak swend } loop if (is_double) { return double(sec(0)) } else { return int(sec(0)) } return #deffunc local import str f stack pri, 100 stack sec, 50 target = f val_tmp = "" is_val = 0 // トークンが数値であるかどうか // 文字列の解析 repeat strlen(target) token = strmid(target,cnt,1) // 数字の場合 token_c = peek(token, 0) if ('0' <= token_c && token_c <= '9' || token_c == '.') { val_tmp += token // val_tmpに数値リテラルを作成する is_val = 1 continue } // 数字と演算子の境で、val_tmpを積む if (is_val) { push pri, val_tmp val_tmp = "" } is_val = 0 // 演算子 // 括弧は積むだけ if (token == "(") { push sec, token continue } // 対応する括弧までの演算子を移動する if (token == ")") { while(sec(sec_i-1) != "(") push pri, pop(sec) wend sec_i-- continue } // 演算子の優先順序の処理 if (sec_i > 0) { if (to_ope(sec(sec_i-1)) > to_ope(token)) { repeat sec_i if (sec(sec_i-1) == "(") :break push pri, pop(sec) loop } } // 積む push sec, token loop // 数値リテラルが余っていれば積んどく if (is_val) { push pri, val_tmp } // 残りの演算子を移動する repeat sec_i push pri, pop(sec) loop return #defcfunc local to_ope str ope // 演算子の判定 switch(ope) case "~" return XOR_ case "|" return OR_ case "&" return AND_ case "<" return LESS case ">" return GRTER case "=" return EQUAL case "+" return ADD case "-" return SUB case "*" return MULT case "/" return DIV case "^" return POW case "(" case ")" return PAREN swbreak swend return UNKNOWN #global }}} * sample.hsp {{{ pi = calc("4*(1-1/3+1/5-1/7+1/9-1/11+1/13-1/15+1/17-1/19+1/21-1/23+1/25)") mes "PI="+pi mes e = calc("1+1/1+1/(1*2)+1/(1*2*3)+1/(1*2*3*4)+1/(1*2*3*4)+1/(1*2*3*4*5)") mes "E="+e mes cos1 = calc("1-1/(1*2)+1/(1*2*3*4)-1/(1*2*3*4*5*6)+1/(1*2*3*4*5*6*7*8)") mes "COS(1)="+cos1 sin1 = calc("1-1/(1*2*3)+1/(1*2*3*4*5)-1/(1*2*3*4*5*6*7)+1/(1*2*3*4*5*6*7*8*9)") mes "SIN(1)="+sin1 mes "COS^2(1)+SIN^2(1)="+calc(strf("%f^2+%f^2", cos1, sin1)) mes mes "2^2^2^2="+calc("2^2^2^2") mes mes "(2^4=4^2)&(5^3<3^5)="+calc("(2^4=4^2)&(5^3<3^5)") mes mes "(1~(1&0))=((1~1)|(1~0))="+calc("(1~(1&0))=((1~1)|(1~0))") }}}